2022/05/悬线法

适用场景

可用于求解给定矩阵中满足某条件的极大矩阵（最大子矩阵）。设矩阵为$N\times M$ ，算法复杂度为$O(N\times M)$ 。

悬线法思想及实现

若在一个矩形区域内寻找满足某条件的最大子矩阵。

悬线，就是一个竖线，这个竖线可以理解为一个具有端点坐标(x,y)、长度L概念的线段。我们将这个悬线进行左、右方向的平移，保证扫过的区域都符合要求，扫过的区域，就可以看做是一个满足条件的子矩阵。

设up[x][y] 为从$(x,y)$ 位置向上符合条件的最长线段长度。

设L[x][y]为从$(x,y)$ 位置向左符合条件的最长线段长度。

设R[x][y]为从$(x,y)$ 位置向右符合条件的最长线段长度。

维护方式：

up[x][y]=up[x-1][y]+1;
L[x][y]=L[x][y-1]+1;
R[x][y]=R[x][y+1]+1;

之后为了计算子矩形，我们需要知道，从$(x,y)$ 向上出发的悬线，左、右各能移动多远。这样我们就能确定一个矩形的面积了。

向上的悬线长度就为矩形的宽，向左、向右的长度加起来就为矩形的长。

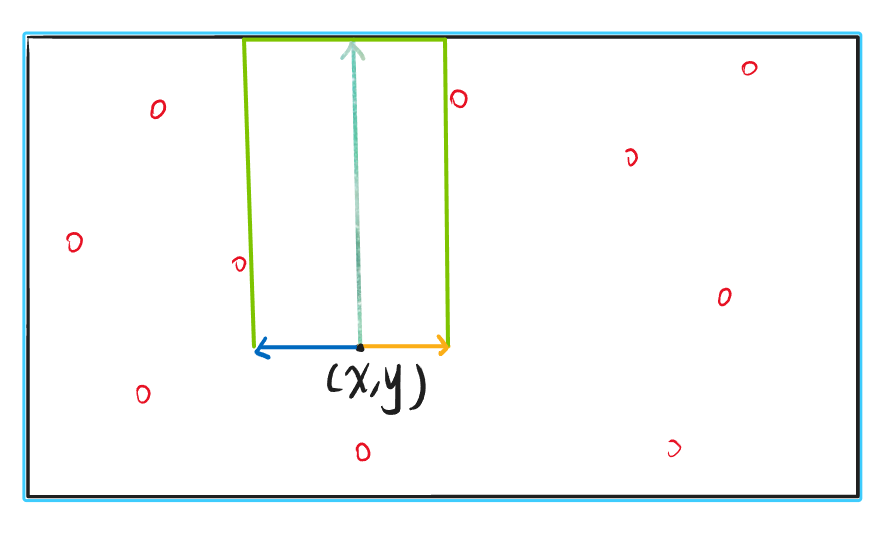
但是，现在需要处理一个问题，如何知道从$(x,y)$向上出发的最长悬线，向左、右各自最长能平移多远。原来L、R中记录的是从某点向左、右方向满足条件的线段的最长长度，并不是悬线的平移长度。

观察下图：

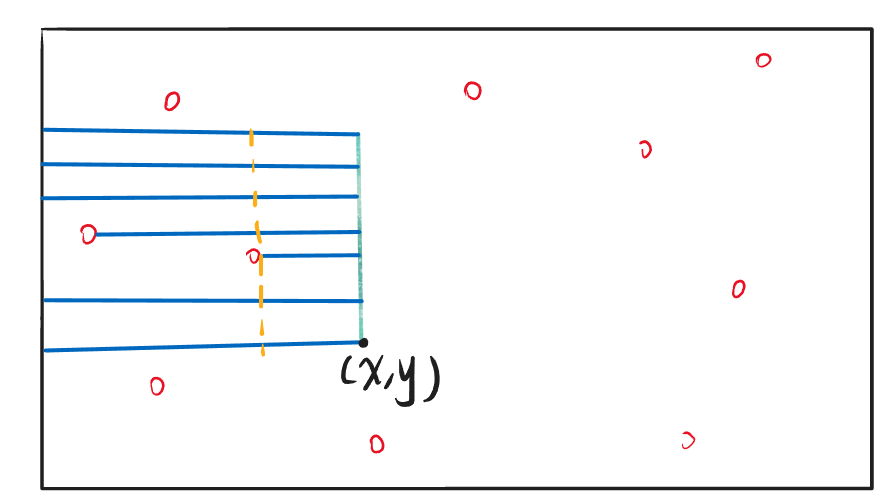
蓝色线段是原来的L数组中存放的内容。而黄色虚线部分则是标记出了，悬线能平移的最远距离。$(x,y)$对应悬线左移的最远距离取决于以该悬线为轴，所有向左能到达的最远距离中最短的距离。

那么我们可以将L[x][y] 更新为从(x,y)位置向左，悬线能平移的最长距离。

$L[x][y]=min(L[x-1][y],L[x][y])$

对应的，R[x][y]也更新为(x,y)位置向右，悬线能平移的最长距离。

$R[x][y]=min(R[x-1][y],R[x][y])$

维护方式：

for(int i=1;i<=n;i++){
    for(int j=1;j<=m;j++){
        if(i>=2 && a[i][j]与a[i-1][j]属于同一悬线){
            L[i][j]=min(L[i-1][j],L[i][j]);
            R[i][j]=min(R[i-1][j],R[i][j]);
        }
    }
}

当确定点的位置$(x,y)$的时候，可以确定以下信息：

1. 从该点除法向上延伸的悬线长度
2. 从该点位置向左，悬线能平移的最长距离
3. 从该点位置向右，悬线能平移的最长距离

由以上的三个信息就能确定由该悬线扫过的区域组成的矩形面积：$up[x][y]*(L[x][y]+R[x][y]-1)$ 。

整体时间复杂度为$O(N\times M)$

模板例题

• 玉蟾宫 题解
• 棋盘制作 题解